Hexágonos (Por David I.)

Como a los alumnos/as les costaba bastante trabajo construir un hexágono a partir de una circunferencia, hicimos una composición a partir de un hexágono inicial. Cada uno de los vértices de dicho hexágono fue el centro de una nueva circunferencia en la que trazamos un nuevo hexágono. Así conseguimos construir en total 7 hexágonos.

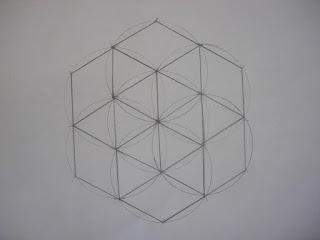
Es bastante difícil este dibujo, pero quería mostraros cómo David I. hizo un trazado perfecto que después coloreó. ¿Verdad que es genial el resultado? ¡Intentad hacer uno igual! Es difícil, pero bastante divertido y el resultado es sorprendente.

Nota de Gregorio: vamos a agradecer al IES ALMERAYA el comentario que hacen a este artículo y es que discrepan en el número de hexágonos. Si veis los comentarios le he contestado pero considero bueno repetirlo aquí por ser de bastante interés: "llevas toda la razón. Dijimos que eran 7 hexágonos porque la construcción partía de uno central más los 6 generados en cada uno de los vértices. Pero además, coincidiendo en tu observación, se genera uno de mayor tamaño que engloba a los 7 restantes. Por ello, son 7 menores más 1 mayor: 8 en total. (¡Qué bien! Nos ha salido uno gratis). Por supuesto, daré la información a los alumnos/as del aula. Comentarios tan enriquecedores nos hacen crecer.